資料3
動的計画法 (Dynamic Programming)
1. 動的計画法とは?
動的計画法(英:”Dynamic Programming”)は、1953年にベルマン氏が提案したプログラミング手法です.
目的とする問題をより小さな部分問題の解を利用して解いていく手法である.その際,部分問題の解を逐次記録ておき,途中で同じ問題が現れた時に記録してある解を利用することで計算の重複を防ぎ,全体の計算量を削減しようというアイデアである.
例えば、フィボナッチ数列で考えてみましょう。定義は下記となります:
fib(1) = 1
fib(2) = 1
fib(n+2) = fib(n+1) + fib(n) (3 <= n)
fib(5)を計算するために,fib(4)とfib(3)を計算する必要があります.
fib(4)を計算するために,fib(3)とfib(2)を計算する必要があります…
それぞれの参照を下記の図に示します.重要なポイントはそれぞれの参照が重複しているとのことです. 元々の問題を分ける時に部分問題が全部独立していれば,動的計画法ではなく,分割統治法(英:Divide and Conquer)になります.
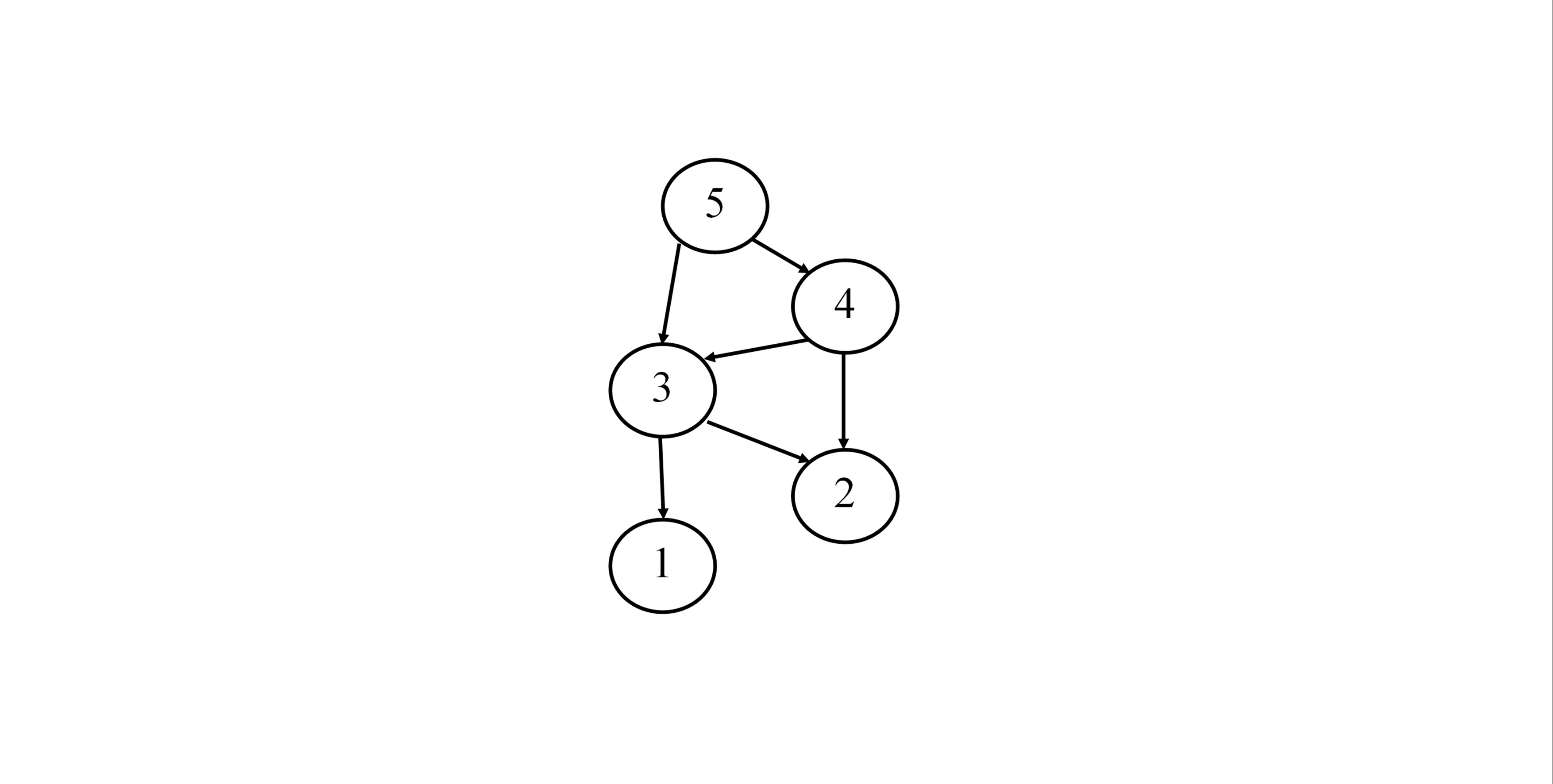
動的計画法で fibonacci を計算する時に,
- fib(1) を fib(3) を計算するために使います.
- fib(2) を fib(3) と fib (4) を計算するために使います.
- fib(n) を fib(n+1) と fib (n+2) を計算するために使います(
2 <= n)
2. 例から学びましょう,Backgammon問題
Backgammon問題は2007 ACM International Collegiate Programming Contest, Asia Reginal Contestのものです. 翻訳は下記
ボードは 0(スタート)から、N(ゴール、5 <= N <= 100)まで.
目的は、ゴールにたどり着くこと.
サイコロを振って、目の数だけ進む.
ゴールを超えた場合はその分戻る.
特別なルールが2つある、LとB
- L:Lose one turn 一回休む
- B:Back to the start スタートに戻る
下の図では,そのルールに従って6ステップでゴールにたどり着く.
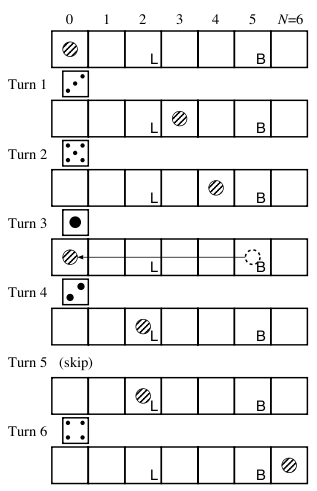
問題 任意のボードに対して、任意 S ステップ以内でゴールにたどり着く確率は?
2.1 Greedy Approach
一つの解決方法として, T 長さのサイコロ連鎖のすべての組み合わせを試してみる.
例えば T = 5 な場合:
- 連続で11111 投げた場合
- 連続で11112 投げた場合
- 連続で11113 投げた場合
- 連続で11114 投げた場合
- 連続で11115 投げた場合
- 連続で11116 投げた場合
- 連続で11121 投げた場合
- …
- 連続で666666 投げた場合
ただ組み合わせが多いです! 計算してみれば 6^5 = 7776 組み合わせがあります. 計算機がまだ解ける範囲ですが,最大 T = 100 な場合は 6^100 ~= 6.5 + 10^77 組み合わせがあります. 無理です.(実際にはすべての組み合わせを計算する必要はありません.並列的に処理することも可能です.)
他の方法がありませんか…
2.2 動的計画法を応用する
解決方法は色々ありますが,下記のように考えてみましょう:
ステップ s の時点で,どの確率でタイル n に至るかを p(s,n) と定義する
最初に(ステップ0の時点で)確実にスタートにいる:
- p(0,0) = 1.0
- p(0,1) = 0.0
- p(0,2) = 0.0
- …
- p(0,N) = 0.0
ステップ s の状況から,s+1 ステップの状況を求める**
2.2.1 プログラムの実装
アルゴリズムの流れ
- Initialization 2次元の配列
pを用意する.この配列にステップ s で t タイルに至る確率をp[s][t]に記録します.最初にp[0][0]=1.0,その他のp[i][j]=0.0. - Main loop ループで示された最大のステップ数 _S_まで,
p[s][*]の確率から,p[s+1][*]の確率を求める. - End 回答を計算する:各ステップ s でゴールにたどり着く確率
p[i][N]を合計する.
B(Back to start)タイルの扱い
例として,ボードの 5 タイル目は,Bタイルであることを前提する.
その場合は,p[s+1][5] ではなく,p[s+1][0] に6分の1の確率を追加する.
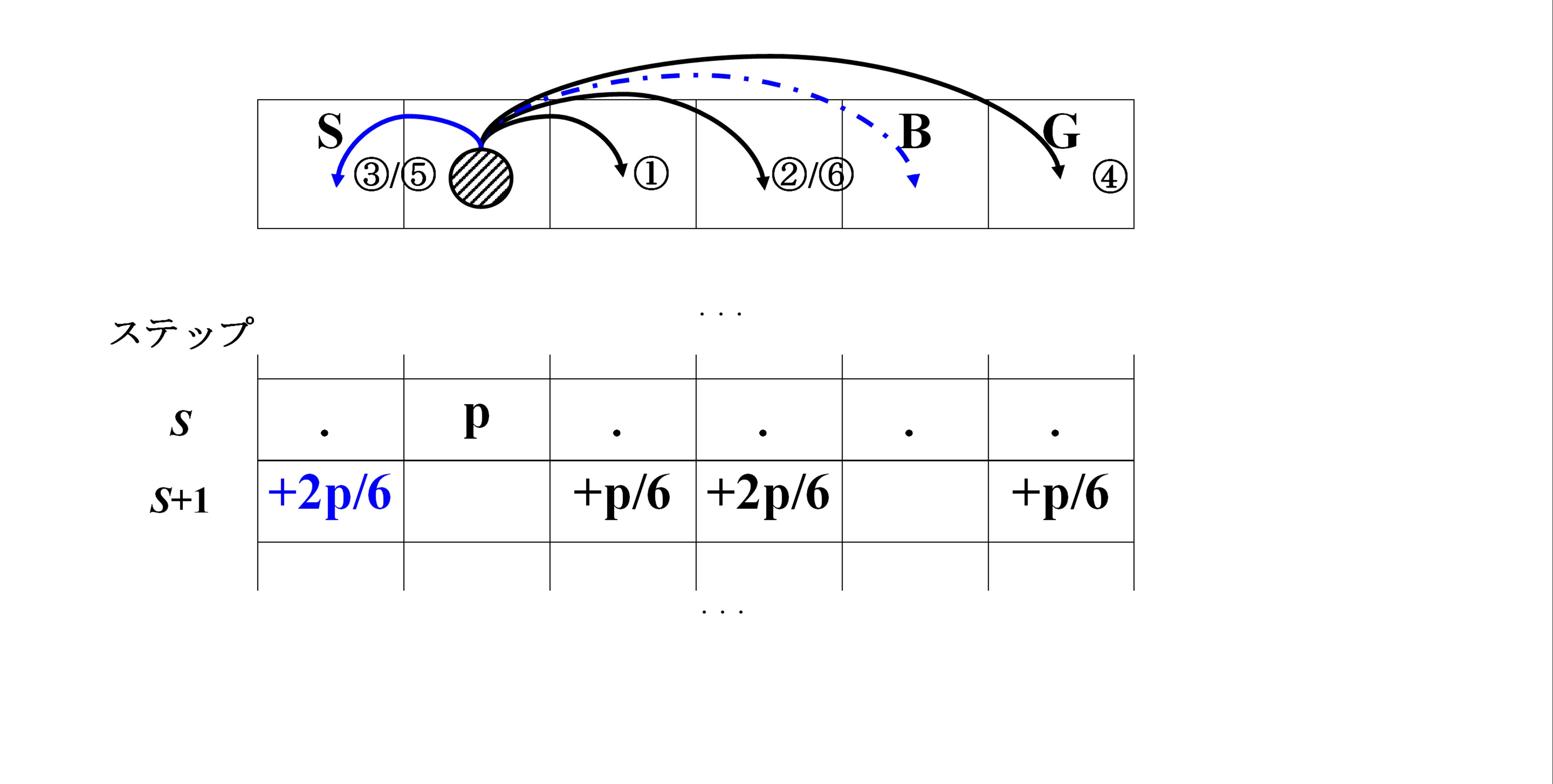
L(Lose one turn)タイルの扱い
本体ならば,ステップ s の状況からステップ s+1 の状況を求める.
ただ,Lのタイルに着いた場合は,次に動くのはのステップではなく,次の次のステップとなる. だから,確率を p 配列に追加する時に,p[s+1][*] ではなく,p[s+2][*] に追加する.
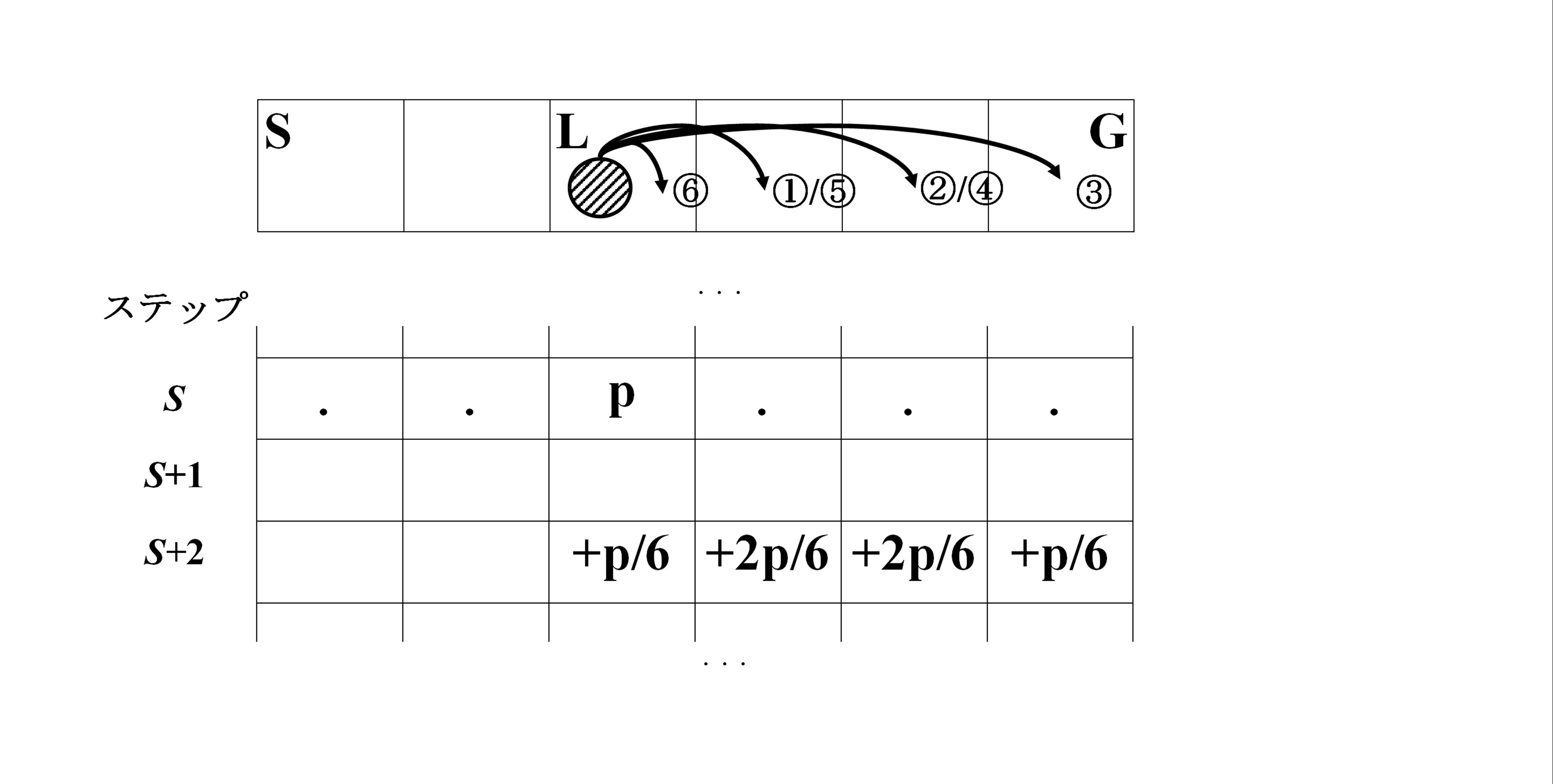
ソースコード
コードはdp/backgammon.cにあります. 入力ファイルの処理等を省略した,理解のために必要最小限の情報を下記に添付します:
typedef enum { W, L, B } state_t;
state_t board[MAX_N+1];
/* 確率配列 Probability array */
double prob[MAX_T+2][MAX_N+1];
double solve(int n, int t) {
/* 確率の配列を全部0.0に初期化 Initialize probability array to 0.0 */
int i,j;
for(i=0; i<t+1; i++) {
for (j=0; j<n+1; j++) {
prob[i][j]=0.0;
}
}
/* 最初のステップに、スタートにいる確率は1.0です */
/* At turn 0, we are at the start with probability 1.0 */
prob[0][0] = 1.0;
for(i=0; i<t; i++) { /* iはステップ数です i is the step number*/
for(j=0; j<n; j++) { /* jはボードにおいているところ j is the placement on the board */
int k; /* kはトランプの価値 k is the dice value */
for(k=1; k<=6; k++) {
int nPos = (j+k>n)? 2*n-k-j: j+k; /* ゴールを超えた場合 Check case we go beyong the Goal */
int nStep = (board[nPos]==L)? i+2: i+1; /* 今Lにいるの場合は、+2のステップに動く if on L, we move again in 2 turns */
if(board[nPos]==B) {
/* 着くタイルはBの場合は、スタート(0)に戻る*/
/* If B, the destination tile is the start (0) */
nPos = 0;
}
prob[nStep][nPos] += prob[i][j] / 6.0;
}
}
}
/* 各ステップにゴールにたどり着く確率を合計する Sum the probability to reach the goal at each step */
double result = 0.0;
for(i=0; i<=t; i++) {
result += prob[i][n];
}
return result;
}
2.3 時間・空間 計算量分析
上記のアルゴリズムの計算量を考えてみましょう.
時間計算量
3重ループを書いたので:
- 各サイコロの値:6(定数)
- ステップの数: T
- ボードのサイズ: N
-> O(S*N)
空間計算量
2次元配列を使いましたので O(T*N).
ただもう少し頑張ったら,過去2ステップだけ記録して O(N) も可能.
現実計算機のスペック
先の時間計算量は今のコンピュータを利用すればどれぐらい時間がかかるか考えてみましょう.
- CPU: 数GHz
- 1秒間で数G(10^9)命令をこなす
- 1000命令がかかる処理でも,1秒間で 数M (10^6)回こなせる
- 今回最大入力は100x100なので,一瞬で済む
- メモリ
- RAMは数GBの範囲(最近の超高級計算機ではTBまで)
- キャッシュ(RAMより遅延が短いので,プログラムがその中に入ればうれしい)のサイズは 数MB
- ハードディスクは数TBの程度